Контрольная работа № 3
Уровень 2 (средний). Геометрия 9 класс
КР–3 Вариант 1
- В треугольнике АВС АВ = 6 см, АС = 8 см, а его площадь равна 12√2 см2. Найдите третью сторону треугольника, если известно, что угол А — тупой.
- В треугольнике MNK ∠M = α, ∠N = β, NK = а. Определите стороны треугольника и его площадь.
- В параллелограмме ABCD АВ = 4 см, AD = 5√2 см, ∠A = 45°. Найдите диагонали параллелограмма.
- Четырехугольник ABCD задан координатами своих вершин А(–1; 1), B(3; 3), С(2; –2), D(–2; –1). Найдите синус угла между его диагоналями. (Примечание от администрации сайта. Автор пособия допустил в данном задании опечатку: то ли в задании нужно найти косинус, то ли опечатка сделана в его ответе, см.ниже)
КР–3 Вариант 2
- В треугольнике АВС АВ = 5 см, ВС = 4 см, а его площадь равна 5√3 см2. Найдите третью сторону треугольника, если известно, что угол В — острый.
- В треугольнике КМЕ ∠K = α, ∠M = β, ME = b. Найдите стороны треугольника и его площадь.
- В параллелограмме MNKP MN = 8 см, МР = 7√3 см, ∠M = 30°. Найдите диагонали параллелограмма.
- Четырехугольник MNKP задан координатами своих вершин М(5; –3), N(1; 2), К(4; 4), P(6; 1). Найдите синус угла между его диагоналями.
ОТВЕТЫ на контрольную работу КР-3:
Задания и Ответы на Вариант 1
№ 1. В треугольнике АВС АВ = 6 см, АС = 8 см, а его площадь равна 12√2 см2. Найдите третью сторону треугольника, если известно, что угол А — тупой.
ОТВЕТ: 2√ см.
№ 2. В треугольнике MNK ∠M = α, ∠N = β, NK = а. Определите стороны треугольника и его площадь.
ОТВЕТ: MN = (a sin(α + β))/sin α,
MK = (a sin β)/sin α,
S = (a2 sin(α + β) sin β) / (2 sin α).
№ 3. В параллелограмме ABCD АВ = 4 см, AD = 5√2 см, ∠A = 45°. Найдите диагонали параллелограмма.
ОТВЕТ: BD = √26 см, AС = √106 см.
№ 4. Четырехугольник ABCD задан координатами своих вершин А(–1; 1), B(3; 3), С(2; –2), D(–2; –1). Найдите синус угла между его диагоналями.Решение: Найдем координаты векторов АС и DB:
AC = {2–(–1); –2–1} = {3; –3};
DВ = {3–(–2); 3–(–1)} = {5; 4}.
Найдем скалярное произведение DB*AC = 5*3 + 4*(–1) = 15 – 12 = 3
Найдем модуль АС и модуль DB:
|AC| = √ = √ = 3√2;
|DB| = √ = √ = √41.Cos ∠x = (DB*AC)/(|DB|*|AC|) = 3/(3√2*√41) = 1/√82 (или √82/82, или ≈ 0,11).Sin ∠x = √[1 – (1/√82)^2] = √[1 – 1/82] = √[81/82] = 9/√82.ОТВЕТ: Cos = 1/√82, Sin = 9/√82.
Задания и Ответы на Вариант 2
№ 1. В треугольнике АВС АВ = 5 см, ВС = 4 см, а его площадь равна 5√3 см2. Найдите третью сторону треугольника, если известно, что угол В — острый.
ОТВЕТ: √21 см.
№ 2. В треугольнике КМЕ ∠K = α, ∠M = β, ME = b. Найдите стороны треугольника и его площадь.
ОТВЕТ: KM = (b sin (α + β))/sin α,
KE = (b sin β)/sin α,
S = (b2 sin (α + β) sin β)/(2 sin α).
№ 3. В параллелограмме MNKP MN = 8 см, МР = 7√3 см, ∠M = 30°. Найдите диагонали параллелограмма.
ОТВЕТ: NP = √43 см, MN = √379 см.
№ 4. Четырехугольник MNKP задан координатами своих вершин М(5; –3), N(1; 2), К(4; 4), P(6; 1). Найдите синус угла между его диагоналями.ОТВЕТ: 17/(5√13).
Ответы на контрольную работу
от автора пособия (возможны опечатки!):
К-3 Уровень 1 + Ответы
К-3 Уровень 3 + Ответы
Вы смотрели: Контрольная работа № 3 по геометрии в 9 классе «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов» с ответами УМК Атанасян (средний уровень). Урок 38 поурочного планирования по геометрии. Геометрия 9 класс КР-3 Уровень 2. Цитаты использованы в учебных целях.
Смотреть Список всех контрольных по геометрии в 9 классе по УМК Атанасян.
(с) В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 9 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Угол между векторами
Любую пару векторов можно отложить от одной точки. Если при этом вектора не сонаправлены друг с другом, то они образуют некоторый угол. Его и именуют углом между векторами.

Если же пара векторов сонаправлена, то принято считать, что угол между такими векторами составляет 0°.
На рисунке показаны два вектора, a и b. Чтобы определить угол между a и b, надо отложить их от одной и той же точки:
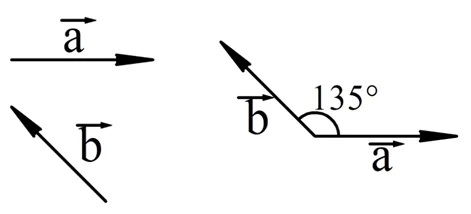
В приведенном примере угол составил 135°. Для обозначения этого угла может быть использована такая запись:
Задание. В квадрате АВСD проведены диагонали, они пересекаются в точке О. Определите, какой угол образуют вектора:

Так как в квадрате диагонали пересекаются под углом 90°, а со сторонами образуют угол 45°, то мы легко определим, что
Здесь нам помог тот факт, что вектора из пунктов а) и б) изначально отложены из одной точки. С пунктом в) ситуация сложнее. Надо отложить от точки А вектор ОА и определить угол, образующийся при этом:

Пусть после откладывания вектора ОА от А получился вектора АА’. Нам надо найти ∠ВАА’. Нам уже известен ∠ОАВ, который является смежным с ∠ВАА’, поэтому можно записать равенство:
Ответ: а) 45°; б) 90°; в) 135°.
Определение перпендикулярности векторов и прямых
Напомним, что скалярное произведение оказывается нулевым исключительно в случае перпендикулярности векторов. Это позволяет использовать его для проверки перпендикулярности векторов.
Задание. Проверьте, являются ли перпендикулярными вектора:
Решение. В каждом случае мы должны скалярно перемножить пару векторов. Если результат окажется нулевым, то можно сделать вывод о перпендикулярности векторов. В противном случае они не перпендикулярны. Первый вектор будет обозначать буквой а, а второй – буквой b:

Ответ: а) да; б) нет; в) да; г) нет.
Задание. При каком значении переменной х вектора а{4; 5} и b{x; – 6} окажутся перпендикулярными?
Решение. Перемножим скалярно вектора и получим некоторое выражение с переменной x:
![]()
Найдем, при каком х это выражение обращается в нуль, то есть вектора становятся перпендикулярными:
Задание. Определите, перпендикулярны ли прямые АВ и CD, если даны координаты точек: А(3; 8), В(4; 10), С(7;12) и D(5;13).
Решение. В этой задаче сначала надорассчитать координаты векторов АВ и CD по координатамих начальной и конечной точки:
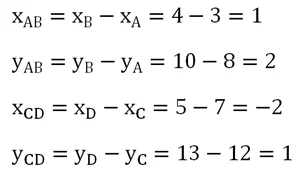
Мы вычислили координаты векторов: АВ{1; 2} и CD{– 2; 1}. Теперь мы можем проверить их перпендикулярность, скалярно перемножив вектора:
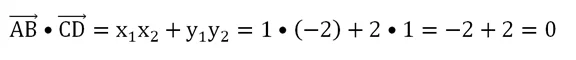
Мы получили ноль. Это означает, что АВ и CD – перпендикулярные вектора. Значит, и прямые, на которых они лежат, также перпендикулярны.
Ответ: перпендикулярны.
Задание. Перпендикулярны ли друг другу прямые, задаваемые уравнениями

Названия точкам в данном примере присвоены произвольно. На следующем шаге по координатам точек мы находим координаты векторов, лежащих на исследуемых прямых:

Полученный ноль показывает, что исходные прямые перпендикулярны.
Ответ: перпендикулярны.
В случае, когда прямые заданы уравнениями, необязательно проделывать столь длительные вычисления для определения их перпендикулярности. Есть теорема, сокращающая объем вычислений.

Докажем это утверждение. Пусть две прямые заданы уравнениями
Найдем какие-нибудь точки этих прямых. Для этого подставим в уравнения значения х = 0 и х = 1:

Прямые окажутся перпендикулярными исключительно в том случае, если это выражение будет нулевым. Это условие перпендикулярности можно записать как уравнение:
В результате мы получили доказываемую нами формулу.
Задание. Проверьте, какие из этих пар прямых перпендикулярны:

Решение. В каждом случае надо просто перемножить угловые коэффициенты прямых, то есть числа, стоящие перед переменной х. Другие числа в этих уравнениях (свободные коэффициенты) никак не влияют на перпендикулярность. Если вычисленное произведение окажется равным (– 1), то из этого будет вытекать перпендикулярность прямых.
























