Основная теорема Шеннона о кодировании
Важный практический вопрос при обработке информации — какова мощность системы передачи данных. Можно получить определённый ответ, используя уравнение Шеннона. Оно позволяет точно понять информационную пропускную способность любого сигнального канала. Формула Шеннона в информатике: I = — (p1log2 p1 + p2 log2 p2 +. + pN log2 pN)
Основная теория Шеннона о кодировании для дискретного канала с помехой, приведённая здесь без доказательства, аналогична теореме канала не имеющего помех: если источник данных с энтропией H (Z), а канал связи имеет ширину полосы C, то сообщения, сгенерированные источником, всегда могут быть закодированы так, чтобы их скорость передачи vz была произвольно близка к значению: vzm = C | H (Z).
Не существует метода кодирования, который бы позволял передавать со скоростью, превышающей vzm, и с произвольно низкой вероятностью ошибки. Другими словами, если поток информации: H ‘(Z) = vz * H (Z) <= C. Тогда можно выбрать специальный код, что позволяет передавать всю информацию с произвольно низкой вероятностью ошибки. При H ‘(Z)> C он не существует.
Используя идею межсимвольного влияния, можно сказать, что, поскольку нет избыточности значения будут независимыми при условии, и они достаточно далеки друг от друга, чтобы их стоило отбирать отдельно. По сути, невозможно сказать, что одно из значений просто от знания другого. Конечно, для любого сообщения оба типа данных заранее определяются содержанием.
Но получатель не может знать, какое из всех возможных сообщений прибыло, пока оно не пришло. Если приёмник заранее знает, какое напряжение, должно быть, передано, то само сообщение не дало бы никакой новой информации! То есть получатель не будет знать больше после его прибытия, чем раньше.
Это приводит к замечательному выводу:
- Сигнал, который эффективно передаёт информацию, будет меняться и непредсказуем.
- Эффективный сигнал очень похож на случайный шум.
Именно поэтому случайный шум может привести к ошибкам в полученном сообщении. Статистические свойства эффективного сигнала аналогичны. Если шум был явно разным, приёмник мог легко отделить информацию и избежать каких-либо неполадок. Поэтому для обнаружения и исправления ошибок нужно сделать реальный сигнал менее «шумоподобным».
Условие применения формулы Шеннона — избыточность, создаёт предсказуемые отношения между различными участками сигнального устройства. Хотя это снижает эффективность передачи информации в системе, но помогает отличать детали сигнала от случайного шума. Здесь обнаружена максимально возможная информационная пропускная способность системы. Поэтому нужно избегать избыточности и позволять сигналу иметь «непредсказуемые» качества, которые делают его статистически похожим на случайный шум.
Передача сигналов
Реальный сигнал должен иметь конечную мощность. Следовательно, для этого набора сообщений должен быть некоторый максимально возможный уровень мощности. Это значит что напряжение тока сигнала ограничено к некоторому ряду. Это также означает, что мгновенное напряжение сигнала, должно быть, ограничено и не выступает за пределы диапазона. Аналогичный аргумент должен быть верен и для шума. Поскольку предполагается, что система эффективна, можно ожидать, сигнал и шум будут иметь аналогичные статистические свойства.
Это означает:
- Если долго наблюдать за сигналом или шумом, можно обнаружить, что их колебания уровня имеют одинаковое отношение пикового/среднеквадратичного напряжения.
- Во время типичного сообщения колебания напряжения шума будут ограничены некоторым диапазоном.
При передаче сигналов в присутствии шума нужно стараться, чтобы сигнал был больше и свести к минимуму эффекты шума. Поэтому можно ожидать, что система передачи информации применится и обеспечит, чтобы для каждого типичного сообщения сила почти равнялось некоторому максимальному значению.
Это означает, что в такой системе, большинство сообщений будет одинаковый уровень мощности. В идеале каждое ИС должно иметь одинаковый, максимально возможный уровень мощности. На самом деле можно повернуть этот аргумент с ног на голову и сказать, что «типичны» только сообщения со средними силами, подобными этому максимуму. Те, что обладают гораздо более низкими способностями, необычны — то есть редки.
Формула Шеннона в информационных потоках
Предыдущий метод не применим для разновероятностных событий. Вероятностный подход подразумевает нахождение этой величины по формуле, предложенной американским математиком Клодом Шенноном и названной в его честь. Данное выражение означает средний объем данных, приходящийся на один выход источника, и обозначается термином энтропия источника сообщений:
\(I=-\sum_{i=1}^Np_i\log_2\left(p_i\right)\)
Значение переменных в данном выражении: I — количество информации; N — число возможных исходов; pi — вероятность события i.
Зависимость событийной вероятности и объема информации можно сформулировать так: чем больше вероятность события, тем меньше информации заключено в сообщении о данном событии.
Подход Шеннона подразумевает под информацией меру сокращения неопределенности.
Примечание
Измерение информации осуществляется в битах. Возможно получение нецелого числа I. При необходимости оценки размера двоичного кода, в который закодирована эта информация, величина I округляется в большую сторону.
Задача 2
При подкидывании неправильной пирамиды с четырьмя гранями вероятности каждого события равняются:
\(p_1=\frac12,\;p_2=\frac14,\;p_3=\frac18,\;p_4=\frac18\)
Найти объем информации при реализации одного из заданных событий.
Решение
Подставим переменные в формулу Шеннона:
\(I=-\sum_{i=1}^Np_i\log_2\left(p_i\right)=-\left(p_1\log_2\left(p_1\right)+p_2\log_2\left(p_2\right)+…+p_N\log_2\left(p_N\right)\right)=-\left(\frac12\log_2\left(\frac12\right)+\frac14\log_2\left(\frac14\right)+\frac18\log_2\left(\frac18\right)+\frac18\log_2\left(\frac18\right)\right)=\)
\(=\left(\frac12+\frac24+\frac38+\frac38\right)=\frac48+\frac48+\frac38+\frac38=\frac{4+4+3+3}8=\frac{14}8=1\frac68=1\frac34=1,75\)
Исходя из этих вычислений, можно сделать вывод: данные, содержащиеся в сообщении после осуществления одного из предполагаемых событий, будет равна 1,75 битам.
Ответ: 1,75 бит.
Вероятностный подход к оценке количества информации
Различные жизненные ситуации обладают различной степенью вероятности. К примеру, при подбрасывании монетки с весовой разницей сторон «орел» и «решка» будут выпадать с различной вероятностью.
Определение
Вероятность случайного события (p) — это отношение количества желаемых исходов данного события (n) к общему количеству исходов (N). Другими словами, p — это коэффициент, указывающий на частоту данного события в результате большого числа идентичных испытаний.
Вероятность может быть выражена числом от 0 до 1 и вычисляется по формуле:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
\(p=\frac nN\)
- при p, равном нулю, событие никогда не случается;
- при p, равном 0,5, событие случается в 50 % от общего числа экспериментов;
- при p, равной единице, событие случается всегда.
Задача 1
На детском празднике в беспроигрышном розыгрыше можно выиграть 2 набора карандашей, 5 раскрасок, 10 шоколадок и 13 наборов пластилина. Необходимо вычислить вероятность выигрыша карандашей.
Решение
1. Сначала найдем общее число исходов. Для этого суммируем все возможные ситуации:
2+5+10+13=20
2. Теперь вычислим искомую вероятность по формуле:
\(p=\frac nN=\frac2{20}=\frac1{10}=0,1\)
Вероятность выигрыша набора карандашей составляет 0,1, то есть карандаши можно выиграть в одном случае из 10.
Ответ: 0,1.
Для определения количества информации в случае равновероятностных событий используют формулу вида:
\(N=2^i\)
Здесь N — число возможных вариантов, показатель степени i означает количество информации.
Определённое уравнение
Сигнал и шум не коррелированны, то есть они не связаны каким-либо образом, который позволит предсказать один из них. Суммарная мощность, получаемая при объединении этих некоррелированных ИС, по-видимому, случайно изменяющихся величин, задаётся.
Поскольку сигнал и шум статистически аналогичны, их комбинация будет иметь то же значение форм-фактора, что и сам сигнал или шум. Потому можно ожидать, что комбинированный сигнал и шум, как правило, будут ограничены диапазоном напряжения.
Стоит рассмотреть теперь разделение этого диапазона на полосы одинакового размера. (т. е. каждая из этих полос будет охватывать ИС.) Чтобы предоставить другую метку для каждой полосы, нужны символы или цифры. Поэтому всегда можно указать, какую полосу занимает уровень напряжения в любой момент с точки зрения B-разрядного двоичного числа. По сути, этот процесс является ещё одним способом описания того, что происходит, когда берут цифровые образцы с B-разрядным аналоговым преобразователем, работающим в общем диапазоне.
Уравнение Шеннона может использовать:
- Максимально возможную скорость передачи информации по заданному каналу или системе.
- Передачу данных определяется полосой пропускания, уровнем сигнала и шума.
- Поэтому ИС называется законом информационной пропускной способности канала.
При передаче информации некоторые параметры используемых сигналов могут приобретать случайный символ в канале связи, например, из-за многолучевого распространения радиоволн, гетеродинирующих сигналов. В результате амплитуда и начальная фаза данных являются случайными. Согласно статистической теории связи, эти особенности сигналов необходимы для их оптимальной обработки, они определяют как структуру приёмника, так и качество связи.
Хартли понимал информационное получение как подбор одного вида данных из набора равновероятного сообщения и определил объём, содержащейся ВС, как логарифм N. Выполняются примеры решения по формуле Хартли в информатике: N = mn.
Помехи разложения всегда присутствуют в границе любого реального сигнала. Однако, если их уровень настолько мал, что вероятность искажения практически равна нулю, можно условно предположить, что все сигналы передаются неискажёнными.
В этом случае средний объём информации, переносимой одним символом, можно считать расчётным: J (Z; Y) = Хапр (Z) — Хапест (Z) = Хапр (Y). Поскольку функция H (Y) = H (Z) и H (Y / Z) = 0, а индекс max {J (Z; Y)} = Hmax (Y) — максимальная энтропия источника класса сигнала, возникающая в результате распределения символов Y: p (y1) = p (y2) = … = p (ym) = 1 / My, т. е. Hmax (Y) = logaMy.
Следовательно, главная дискретная ширина полосы таблицы без информации о помехах в единицу времени равна: Cy = Vy • max {J (Z; Y)} = Vy • Hmax (Y) = Vy • logaMy или записываться Ck = Vk • logaMy. Где буква Mk — должно быть максимально возможное количество уровней, разрешённых для передачи по этому каналу (конечно, может обозначаться Mk = My).
Согласно теореме, метод кодирования онлайн, который может использоваться и позволяет:
- с данными согласно уравнению H (x) ≤ C — передать всю информацию, сгенерированную источником с ограниченным размером буфера калькулятора;
- в случае H (x)> C такого способа кодирования не существует, поскольку требуется буфер, объём которого определяется избыточной производительностью источника по ширине полосы канала, умноженной на время передачи.
3.2. Спектр дискретного сигнала
Перейдем теперь к рассмотрению спектра дискретного сигнала. Очевидно, в соответствии с изложенным выше свойством симметрии преобразования Фурье следует ожидать периодического характера спектральной функции дискретного сигнала.
Итак, дискретный сигнал , как уже подчеркивалось выше, формируется на выходе перемножителя, на один вход которого, подается непрерывный сигнал , а на второй – периодическая последовательность коротких импульсов длительностью
,
с периодом .
Здесь – функция, определяющая форму импульсов периодической последовательности. Обычно в качестве периодической последовательности импульсов дискретизации выбирают импульсы прямоугольной формы вида (1.13). Периодическую последовательность импульсов дискретизации можно описать выражением
.
Тогда дискретный сигнал запишется в виде
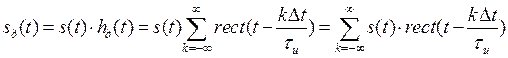. (3.11)
С другой стороны, последовательность прямоугольных импульсов может быть представлена комплексным рядом Фурье
. (3.12)
Здесь учтено, что период последовательности равен , амплитуда единичного импульса , а также .
Теперь можно представить с учетом (3.12) в виде ряда
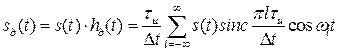. (3.13)
Применим к (3.13) прямое преобразование Фурье
.
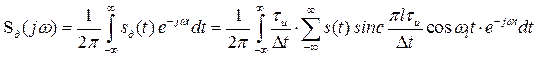Изменив порядок суммирования и интегрирования, запишем
. (3.14)
Так как
,
то
.
В свою очередь
,
.
Тогда окончательно выражение (3.14) принимает вид
. (3.15)
Спектральный анализ дискретного сигнала существенно упрощается, если предположить, что дискретизация осуществляется последовательностью прямоугольных импульсов единичной площади. В этом случае амплитуда импульса и выражение (3.15) запишется следующим образом
.
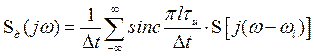Если устремить к нулю при сохранении единичной площади импульса и перейти к последовательности бесконечно коротких импульсов ( -импульсов), т.е.
, (3.16)
то
,
а спектральная функция дискретного сигнала примет вид
. (3.17)
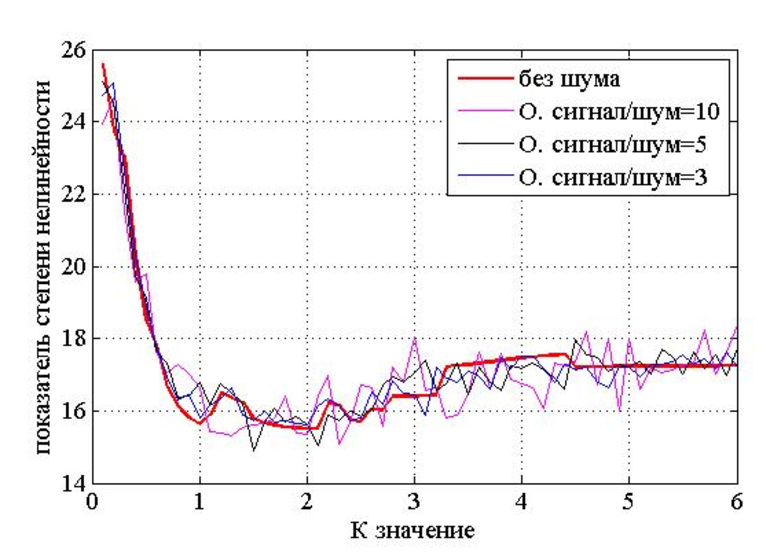
На рис. 3.5, а представлен непрерывный сигнал , а на рис. 3.5, б – условное изображения модуля его спектральной функции .
Как известно, спектр непрерывного одиночного сигнала является сплошным.
Спектр же дискретного сигнала, как это следует из (3.16), представляет собой периодическую по частоте последовательность копий спектров исходного сигнала, сдвинутых относительно друг друга на величину (или ), что составляет период последовательности. Очевидно, периодическим по частоте с тем же периодом является и модуль спектра и его аргумент, т.е. фазовый спектр.
Отметим, что (или ) – это частота дискретизации. Таким образом, период спектральной функции дискретного сигнала равен частоте дискретизации. На рис. 3.5. в, г изображены графики дискретного сигнала и модуля его спектра.
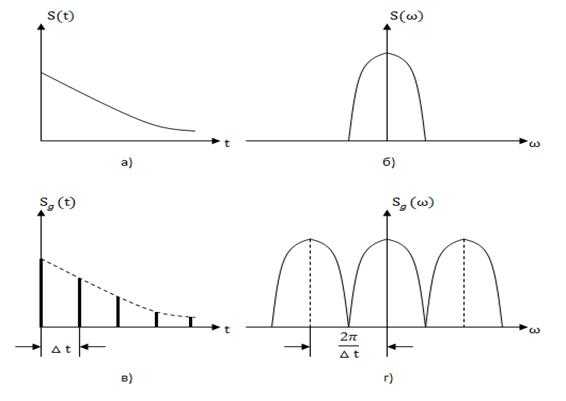
Рис. 3.5
Расположение отдельных составляющих периодической функции спектра дискретного сигнала на оси частот зависит от значения частоты дискретизации . На рис. 3.5,г и на рис. 3.6, а, б изображены соответственно функции дискретного сигнала при частотах дискретизации (или ), (или ) и (или ). Из этих рисунков следует, что при частоте дискретизации, меньшей чем частота, определяемая пределом Найквиста, копии спектра исходного непрерывного сигнала перекрываются, т.е. имеет место явление наложения спектров. Это приводит к искажению исходного сигнала при его восстановлении. Таким образом, и спектральный анализ дискретного сигнала согласуется с выводами теоремы Котельникова.
Информационная теория
Обработка информации — важная техническая задача, чем, например, преобразование энергии из одной формы в другую. Важнейшим шагом в развитии теории информации стала работа Клода Шеннона (1948). Логарифмическое измерение количества данных было первоначальной теорией, и прикладными задачами по коммуникации в 1928 году. Наиболее известным является вероятностный подход к измерению информации, на основе которого представлен широкий раздел количественной теории.
Отличительная черта вероятностного подхода от комбинаторного состоит в том, что новые предположения об относительной занятости любой системы в разных состояниях и общего количества элементов не учитываются. Ряд информации взят из отсутствия неопределённости в выборе различных возможностей. В основе такого подхода лежат энтропийные и вероятностные множества.
Теорема Шеннона-Хартли
При рассмотрении всевозможных многоуровневых и многофазных способах шифрования, утверждение Шеннона-Хартли звучит следующим образом.
Теорема
Пропускная способность канала (С), являющаяся верхним пределом передачи данных, передаваемых со средней мощностью сигнала (S) через аналоговый канал, на который воздействует гауссовский шум с мощностью (N), вычисляется так:
\(C=B\log_2\left(1+\frac SN\right)\)
Здесь: С — пропускная способность канала (бит/с), B — полоса пропускания канала (Гц), S — полная мощность сигнала над полосой пропускания (Вт или В2), N — полная шумовая мощность над полосой пропускания (Вт или В2).
Согласно рассматриваемой теореме, максимальная скорость достигается посредством расширения пропускной полосы и усилении мощности сигнала при уменьшении шума. Иными словами, скорость увеличится, если обеспечить преобладание уровня полезного сигнала над шумом.
При существовании аналогового канала с отсутствием шума и неограниченной полосой пропускания возможность передачи данных без искажения за определенное время не ограничена в объеме. В реальности таких каналов не бывает: они имеют лимит по частоте и характеризуются наличием шума.
Теорема Шеннона-Хартли берет во внимание присутствие шума в канале и предполагает, что приемник воспринимает комплекс из сигналов и шума. Это сочетание необходимой информации и случайного шума кодируется и распознается устройством
Понимания присутствия шума дает возможность получить оригинальную информацию при декодировании.
Значение
Выведем формулу эффективного числа M. Для этого выполним сравнение пропускной способности и меры Хартли:
\(2B\log_2\left(M\right)=B\log_2\left(1+\frac SN\right)\)
\(M=\sqrt{1+\frac SN}\)