Алгебра 9 класс

Алгебра 9 класс (Мерзляк) Самостоятельная работа № 1. Вариант 1.

С-01 «Числовые неравенства» (транскрипт заданий)

1. Сравните числа а и b, если: 1) а – b = –0,3; 2) а – b = 1,2;   3) а = 0,6 + b;   4) b = а – 8.
2. Точка A (а) расположена на координатной прямой правее точки В (–2). Какое из утверждений верно: 1) а > –2; 2) а < –2;   3) а = –2;   4) числа a и –2 сравнить невозможно?
3. Докажите неравенство: 1) (а – 8)(а + 7) > (а + 10)(а –11); 2) (а – 6)2 – 2 < (а – 5)(а – 7); 3) (2а – 5)(2а + 5) – (3а – 2)2 ≤ 3(4а – 9) – 2.
4. Докажите неравенство: 1) а2 – 6а+ 10 > 0; 2) 12y – 4y2 – 11 < 0; 3) а(а – > 2(а –13);   4) х2 + 4y2 + 6х + 4y + 10 ≥ 0;   5) х2 – 10xy + 26y2 + 12у + 40 > 0;   6) (a2+5) / √ ≥ 2.
5. Докажите, что: 1) ab(a + b) ≤ a3 + b3, если а ≥ 0, b ≥ 0; 2) m3 + m2 – m – 1 > 0, если m > 1.
6. Докажите, что: 1) (а + b)(1/a + 1/b) ≥ 4, если а > 0, b > 0; 2) (а + 6)(b + 3)(с + 2) ≥ 48√, если а ≥ 0, b ≥ 0, с ≥ 0.

Примечание: в квадратных скобках — выражение или число, находящиеся под действием арифметического корня √.

Алгебра 9 Мерзляк С-01 В1.ОТВЕТЫ на самостоятельную работу:

№ 1. 1) а – b = –0,3  ⇒  а < b ;   2) а – b = 1,2  ⇒  а > b ;   3) а = 0,6 + b  ⇒  а > b ;  4) b = а – 8  ⇒  а > b.

№ 2.   а > –2  ⇒  верно.

№ 3. 1) (а – (а + 7) > (а + 10)(а – 11)   ⇒  а2– а – 56 > а2– а – 110   ⇒   –56 > –110  ⇒  верно. 2) (а – 6)2 – 2 < (а – 5)(а – 7)   ⇒  а2– 12а + 36 – 2 < а2– 12а + 35   ⇒  34 < 35  ⇒  верно. 3) (2а – 5)(2а + 5) – (За – 2)2 ≤ 3 • (4а – 9) – 2   ⇒  4а2– 25 – 9а2 + 12а – 4 ≤ 12а – 27 – 2   ⇒  –5а2 < 0  ⇒  верно.

№ 4. 1) а2– 6а + 10 > 0   ⇒  а2–6а + 9 + 1>0   ⇒   (а – 3)2 + 1 > 0  ⇒  верно. 2) 12у – 4у2– 11 < 0   ⇒  –(4у2– 12у + 9 + 2) < 0   ⇒  – ((2у – З)2 + 2) < 0  ⇒  верно. 3) а(а – > 2 • (а – 13)   ⇒  а2– 8а > 2а – 26   ⇒  а2– 2а – 8а + 26 > 0   ⇒  а2– 10а+ 26 + 1 > 0   ⇒  (а – 5)2 + 1 > 0  ⇒  верно. 4) х2 + 4у2 + 6х + 4у + 10 ≥ 0   ⇒  (х2 + 6х + 9) + (4у2 + 4у + 1) ≥ 0   ⇒  (х + З)2 + (2у + 1)2 ≥ 0   ⇒  верно. 5) х2– 10ху + 26у2 + 12у + 40 > 0   ⇒  (х2– 10ху + 25у2) + (у2 + 12у + 36) + 4 > 0   ⇒  (х – 5у)2 + (у + 6)2 + 4 > 0   ⇒  верно. 6) ((a2+5) / √)2 ≥ 4   ⇒ (a4 +10a2 + 25)/(a2 + 4) ≥ 4   ⇒ (a4 + 10a2 + 25 – 4a2 – 16)/(a2 + 4) ≥ 0   ⇒ (a2 + 3)2/(a2 + 4) ≥ 0   ⇒ верно.

№ 5. 1) ab(a + b) ≤ а3 + b3, а ≥ 0, b ≥ 0 ab(a + b) ≤ (а + b)(a2– ab + b2)   ⇒  ab(a + b) – (а + b)(а2– ab + b2) ≤ 0   ⇒  (а + b)(ab – a2 + ab – b2) ≤ 0   ⇒  –(а + b)(а – b)2 ≤ 0   ⇒  а + b ≥ 0, (а – b)2 ≥ 0  верно.

2) m3 + m2– m – 1 > 0, m > 1 m2(m + 1) – (m + 1) > 0   ⇒  (m + 1)(m2– 1) > 0   ⇒  (m + 1 )(m + 1)(m – 1) > 0   ⇒  (m + 1)2(m – 1) > 0   ⇒  верно (m – 1 > 0 т.к. m > 1;   (m + 1)2 > 0 всегда).

№ 6. 1) ((а + b)(b + а))/ab ≥ 4  ⇒ (a + b)2/ab ≥ 4  ⇒ (a2 + b2 + 2ab – 4ab)/ab ≥ 0   ⇒ (а – b)2/ab ≥ 0   ⇒  верно (ab > 0 т.к. а > 0, b > 0;   (а – b)2 > 0 всегда).

2) ((а + 6)(b + 3)(с + 2)) / 8 – 6√ ≥ 0   ⇒ √6a • √3b • √2c – 6√ ≥ 0  ⇒ √ – 6√ ≥ 0  ⇒  6√ – 6√ > 0   ⇒ верно.

Вы смотрели: Самостоятельная работа по алгебре в 9 классе «Числовые неравенства» с ответами. Дидактические материалы для учителей, учащихся и родителей. Алгебра 9 Мерзляк С-01 В1.

Перейти к Списку контрольных работ по алгебре в 9 классе УМК Мерзляк.

Цитаты (упражнения) из учебного пособия «Дидактические материалы. Алгебра 9 класс / Мерзляк, Полонский, Рабинович, Якир — М.:Вентана-Граф» использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Решения и ОТВЕТЫ на самостоятельную работу (нет в пособии) адресованы родителям для проверки знаний учащихся.

Алгебра 9 класс (Мерзляк) Задание № 1 «Проверьте себя»

№ 1. Сравните числа а и b, если а – b = –3,6.
А) а > b;   Б) а < b;   В) а = b;   Г) сравнить невозможно

Решение: а — b = —3,6   ⇒   а = 6 — 3,6   ⇒   а < b
Правильный ответ: Б.

№ 2. Известно, что m > n. Какое из данных утверждений ошибочно?
А) m – 2 > n – 2; Б) 2m > 2n;  B) m + 2 > n + 2; Г) –2m > –2n.

Решение: m > n   ⇒   —2m > —2n   ⇒   неверно, —2m < —2n
Правильный ответ: Г.

№ 3. Оцените периметр Р равностороннего треугольника со стороной а см, если 0,8 < а < 1,2.
А) 1,6 см < Р < 2,4 см;   В) 3,2 см < Р < 4,8 см;
Б) 2,4 см < Р < 3,6 см;   Г) 1,2 см < Р < 1,8 см.

Решение: 0,8 < а < 1,2   ⇒   2,4 < 3а < 3,6
Правильный ответ: Б.

№ 4. Известно, что 2 < x < 3 и 1 < y < 4. Оцените значение выражения ху.
А) 4 < хy < 8;   Б) 3 < xy < 7;   В) 2 < хy < 12;   Г) 6 < xy < 14.

Решение: 2 < х < 3 и 1 < у < 4  ⇒   2 < х < 3•1 < у < 4   ⇒   2 < ху < 12
Правильный ответ: В.

№ 5. Известно, что –18 < y < 12. Оцените значение выражения y/6 + 2.
А) –3 < у/6 + 2 < 4;   Б) –1 < у/6 + 2 < 4;   В) –1 < у/6 + 2 < 2;   Г) –3 < у/6 + 2 < 2.

Решение: –18 < у < 12   ⇒  –3 < y/6 < 2   ⇒  –1 < у/6 + 2 < 4
Правильный ответ: Б.

№ 6. Дано: а > 0, b < 0. Какое из данных неравенств может быть правильным?
А) а2 < b2;   Б) a/b > 1;   В) а – b < 0;   Г) a2b3 > 0.

Решение:  а > 0, b < 0   ⇒   а2 < b2   ⇒ может быть правильным.
Правильный ответ: А.

№ 7. Множеством решений какого неравенства является множество действительных чисел?
А) 2х > –2;   Б) 2х > 0;   В) 0х > –2;   Г) 0х > 0.

Решение:  0 • х > –2   ⇒   х — любое число.
Правильный ответ: В.

№ 8. Множеством решений какого неравенства является промежуток (3; – ∞)?
А) х ≥ 3;   Б) х ≤ 3;   В) х > 3;   Г) х < 3.

Решение: (3; +оо),   x > 3
Правильный ответ: В.

№ 9. Найдите решения неравенства х/4 ≤ 1/5.
A) х ≥ 4/5;   Б) х ≥ 1/20;   В) х ≤ 4/5;   Г) х ≤ 1/20.

Решение: х/4 ≤ 1/5   ⇒   x/4 – 1/5 ≤ 0
(5x – 4)/20 ≤ 0   ⇒   5x – 4 ≤ 0
5х – 4 ≤ 20   ⇒   5х ≤ 4   ⇒   x ≤ 4/5.
Правильный ответ: В.

№ 10. Решите неравенство –3х + 8 > 5.
А) х ≤ 1;   Б) х ≥ 1;   В) х ≤ –1;   Г) х ≥ –1.

Решение: –3х + 8 ≥ 5   ⇒   –3х ≥ —3   ⇒   х ≤ 1
Правильный ответ: А.

№ 11. Найдите наименьшее целое решение неравенства (3x – 5)/2 > (8 – x)/3.
А) 2; Б) 3; В) 4; Г) определить невозможно.

Решение:  (3х – 5)/2 > (8 – х)/3  ⇒  9х – 15 > 16 – 2х   ⇒  11х > 31
х > 31   ⇒   х > 2 9/₁₁
Правильный ответ: Б.

№ 12. Чему равно произведение натуральных чисел, принадлежащих области определения выражения √?
А) 4; Б) 10; В) 18; Г) 24.

Решение: 14 – 3х ≥ 0   ⇒  –3х ≥ -14
х ≤ 14/3   ⇒   x ≤ 4 2/₃
2 • 3 • 4 = 24.
Правильный ответ: Г.

№ 13. Какая из данных систем неравенств не имеет решений?
А) { х ≥ –3, х ≤ –2; Б) { х > –3, х > –2; В) { х ≥ –3, х ≤ –3; Г) { х ≥ –2, х ≤ –3.

Решение: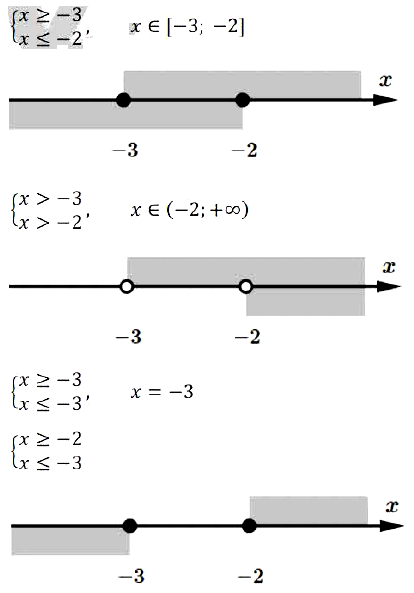
Правильный ответ: Г.

№ 14. Найдите множество решений системы неравенств
{ х – 1 > 2х – 3,
{ 4х + 5 > х + 17.
А) O; Б) (2; +∞); В) (–∞; 4); Г) (2; 4).

Решение: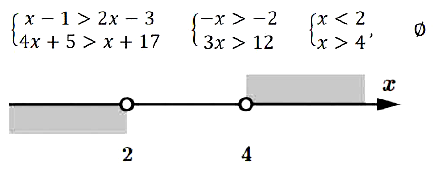
Правильный ответ: А.

№ 15. Какой из изображённых числовых промежутков соответствует множеству решений системы неравенств
{ 8 – 7х > 3х – 2,
{ –2(3х – 2,6) ≤ –2 • (–2,6) ?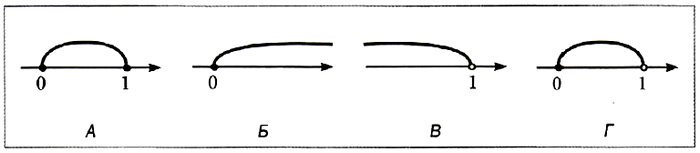

Решение: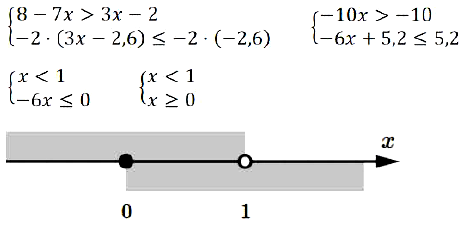
Правильный ответ: Г.

№ 16. Сколько целых решений имеет система неравенств
{ х – (x – 2)/3 ≥ (х – 3)/4 – (х – 1)/2,
{ 1 – 0,5х > х – 4 ?
А) 3;   Б) 4;   В) 5;   Г) 6.

Решение: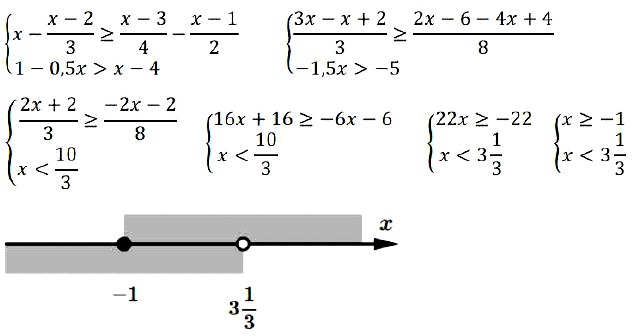
Правильный ответ: В.

№ 17. Решите неравенство –3 < (1 – 2x)/5 – 2 < 1.
А) (–3; 7);   Б) (–7; 3);   В) (–7;–3);   Г) (3; 7).

Решение: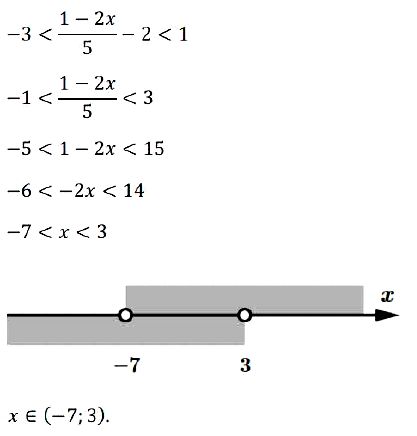
Правильный ответ: Б.

№ 18. При каких значениях а уравнение 2х2 + 6х + а = 0 не имеет корней?
А) а < 4,5;   Б) а > 4,5;   В) а > –4,5;   Г) а < –4,5.

Решение: 2х2 + 6х + а = 0   ⇒   D = 36 — 8а   ⇒   36 — 8а < 0
—8а < —36   ⇒   а > 4,5
Правильный ответ: Б.

Вы смотрели: Алгебра 9 класс УМК Мерзляк. Упражнения из учебника с ответами и решениями. Глава 1. НЕРАВЕНСТВА. Задание № 1 «Проверьте себя» в тестовой форме. Алгебра 9 Мерзляк Тест 1 + ОТВЕТЫ.