Геометрия 10 мерзляк кр-1

Геометрия 10 класс (Мерзляк) Контрольная работа № 1.

КР-1. Вариант 1.

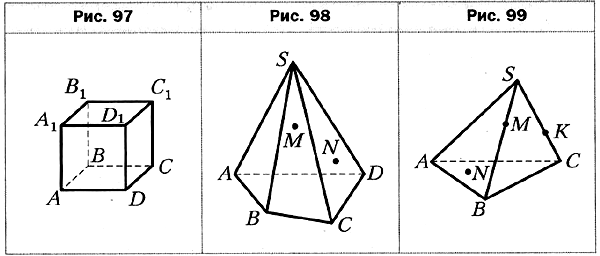
1. На рисунке 97 изображён куб ABCDA₁B₁C₁D₁. Укажите прямую пересечения плоскостей АВ₁С₁ и ABB₁.
2. Даны точки А, В и С такие, что АВ = 2 см, ВС = 5 см, АС = 3 см. Сколько существует плоскостей, содержащих точки А, В и С? Ответ обоснуйте.
3. Точки А, В и С не лежат на одной прямой. На прямой АВ отметили точку D, на прямой ВС — точку В, а на прямой DE — точку М. Докажите, что точки А, С и М лежат в одной плоскости.
4. Точки М и N принадлежат соответственно граням SBC и SCD пирамиды SABCD (рис. 98). Постройте точку пересечения прямой MN с плоскостью SBD.
5. Точки М и К принадлежат соответственно рёбрам SB и SC тетраэдра SABC, а точка N — грани АВС (рис. 99), причём прямые МК и ВС не параллельны. Постройте сечение тетраэдра плоскостью MNK.

КР-1. Вариант 2.

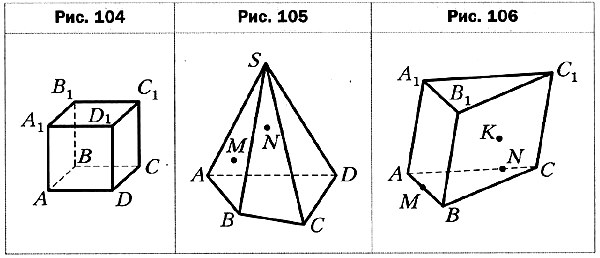
1. На рисунке 104 изображён куб ABCDA₁B₁C₁D₁. Укажите прямую пересечения плоскостей АСС₁ и DCC₁.
2. Даны точки А, В и С такие, что АВ = 4 см, ВС = 6 см, АС = 7 см. Сколько существует плоскостей, содержащих точки А, В и С? Ответ обоснуйте.
3. Прямые а и b пересекаются в точке О. На прямой а отметили точку А, на прямой b — точку B, а на прямой АВ — точку С. Докажите, что прямые а, b и точка С лежат в одной плоскости.
4. Точки М и N принадлежат соответственно граням SAB и SBC пирамиды SABCD (рис. 105). Постройте точку пересечения прямой MN с плоскостью SAC.
5. Точки М и N принадлежат соответственно рёбрам АВ и АС призмы ABCA₁B₁C₁, а точка К — грани ВВ₁С₁С (рис. 106), причём прямые MN и ВС не параллельны. Постройте сечение призмы плоскостью MNK.

ОТВЕТЫ на КР-1 Вариант 1

№ 1. На рисунке 97 изображён куб ABCDA₁B₁C₁D₁. Укажите прямую пересечения плоскостей АВ₁С₁ и ABB₁.ОТВЕТ: AB₁.

№ 2. Даны точки А, В и С такие, что АВ = 2 см, ВС = 5 см, АС = 3 см. Сколько существует плоскостей, содержащих точки А, В и С? Ответ обоснуйте.ОТВЕТ: бесконечное множество.
ОБОСНОВАНИЕ: Из аксиомы стереометрии следует, что через любые 3 точки, не лежащие на 1 прямой, проходит ровно 1 плоскость. Точки А, В и С могут находиться на одной прямой, так как 2 + 3 равно 5 (точка А на прямой ВС).

№ 3. Точки А, В и С не лежат на одной прямой. На прямой АВ отметили точку D, на прямой ВС — точку Е, а на прямой DE — точку М. Докажите, что точки А, С и М лежат в одной плоскости.ДОКАЗАТЕЛЬСТВО: Так как точки А, В, С не лежат на одной прямой, то существует единственная плоскость а, проходящая через эти точки (аксиома стереометрии). То есть, а = (АВС).
Если две точки прямой принадлежат плоскости, то и вся прямая (все точки прямой) принадлежит этой плоскости. Так как точки А и В принадлежат а, то и прямая АВ принадлежит а, и точка D на прямой АВ тоже принадлежит а.
Аналогично, прямая ВС принадлежит а, и точка Е принадлежит а. Из этого следует, что прямая DE также принадлежит плоскости а. Но тогда любая точка этой прямой, в том числе точка М, принадлежит а, что и требовалось доказать.

№ 4. Точки М и N принадлежат соответственно граням SBC и SCD пирамиды SABCD (рис. 98). Постройте точку пересечения прямой MN с плоскостью SBD.ОТВЕТ: Из точки С в заданных гранях через точки M и N проводим прямые до пересечения с плоскостью SBD. Получили прямые СК и СР.
Прямая КР — след пересечения плоскости, проходящей через прямые CK и CP с плоскостью SBD. Прямая КР принадлежит плоскости SBD, так как точки К и Р принадлежат этой плоскости.
Проводим прямую MN до пересечения с прямой КР. Точка О – это точка пересечения прямых MN и KP. Следовательно, точка О – точка пересечения с плоскостью SBD.

№ 5. Точки М и К принадлежат соответственно рёбрам SB и SC тетраэдра SABC, а точка N — грани АВС (рис. 99), причём прямые МК и ВС не параллельны. Постройте сечение тетраэдра плоскостью MNK.ОТВЕТ: Продлить отрезок МК до пересечения с продлением ребра ВС. От этой точки через точку N будет проходить линия пересечения с плоскостью основания. Далее через точки пересечения следа с рёбрами основания проводятся линии сечения.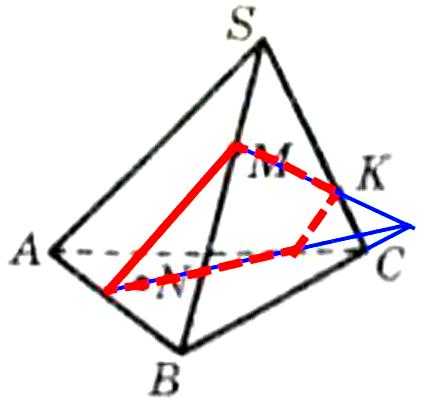

Аналогично решаются задания Варианта 2.

Вы смотрели: Контрольная работа № 1 по геометрии «Аксиомы стереометрии и следствия из них. Начальные представления о многогранниках» для 10 класса (2 варианта) УМК Мерзляк Базовый уровень. Геометрия 10 Мерзляк КР-1 с ответами.

Цитаты из пособия «Дидактические материалы. Геометрия 10 класс. Базовый уровень»  (авт. А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович, М.С.Якир, изд-во «Вентана-Граф») использованы на сайте в незначительных объемах, исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ).